The Bagpipe Society
Cabrette Tuning Yet Again...
It’s good to see the subject of tuning and scales capturing the interest of members, because it’s a subject hard to understand and therefore not well understood. So I was fascinated to turn to Ray Brown’s thoughts on the tuning of the Cabrette in the Winter 2015 edition of Chanter, the third response to Ian Clabburn’s original article in Chanter of Summer 2014. Ray covered a wide range of topics and raised a large number of questions.
But I would like, with all respect to Ray, to offer an alternative point of view with regard to some of his statements and suggestions.
Michel Esbelin is a virtuoso cabrette player who gave a paper on the instrument at the International Bagpipe Symposium at the Hague in 1988 (Ref 1). This is what he says:
“The cabrette’s range is one octave plus one tone and half (without taking into account the lowest note, aligned with the little finger of the right hand and which is used as an articulation or is quite simply there for ornamental purposes). If the instrument is being played in C major (this is the translation from the French, but I think “For an instrument in C major” is a clearer meaning), then we will be working with a scale which starts at G (bottom G) and rises to B flat after one octave.
……………..the fixed notes G, A, C, D, E, G, A constitute a pentatonic scale. The mobile notes B and F in this context create special intervals which provide for rich combinations.
………………The tonic C is a fixed note is always played with great care by the musicians because it comes at the end of most tunes and conveys a feeling of completeness and stability. It is the basic note of our mode. The sub-tonic B (my italics) is, on the other hand, a mobile note and the interval which separates it from the next one is very great. It is a preparatory note, usually played in trill or more often in a rising slide.”
The tuning of the cabrette scale was the issue originally raised by Ian Clabburn, and he refers in particular to what he called the ’neutral third’, and I think it is this which has given rise to some misunderstanding. It is essential to grasp, as above stated by Michel, that on a cabrette chanter where the main scale runs from G to G, the keynote, the tonic, is the three-finger note C. If you close the next hole with the index finger of the lower hand, the note you get is not a third but a leading note. I think it’s clear from this that the B is not to be considered a third in the scale of G, but a leading note in the scale of C. As such the manipulation of this note becomes important in the context of the music and in the formation of a personal style. By contrast, the third in the scale of C, the E, is one of what Michel above calls the fixed notes. I suggest this would be tuned a just third above the C.
In short for these reasons I don’t think that the cabrette can be considered as evidence for the existence of a neutral third in bagpiping.
In the second paragraph of page 2 of his article, Ray suggests that “Originally neutral intonations were probably characteristic of all mouth blown bagpipes including half long pipes (of England), the cornemuse (of central France) and the biniou (of Brittany), among many others.” I don’t know whether this was so or not. But I can throw some light on the case from the experience of Bernard Blanc with old pipes from the centre of France. As France’s leading maker of cornemuses du Centre, he has studied many of the oldest examples. He explained to me that the chanters are rather different from the modern style; in particular, the wall is thicker and the fingerholes are smaller and more equally spaced. This gives a sound and performance closer to a modern cabrette than to a modern Bechonnet style chanter. In addition, closing the top finger of the lower hand does not give a true third, but true major and minor thirds can be got by cross-fingerings, in the manner of many early woodwinds.
We know from early woodwinds that the apparent size and disposition of the fingerholes does not give much help in discovering what kind of scale a particular instrument will play. As one example of this, the recorder was notoriously misinterpreted at the time of Arnold Dolmetsch’s revival of the instrument in the early 20th century, resulting in two systems of fingering in modern reproductions, the so-called English and German systems. Another example is that of the cornetto; at the Galpin Society Conference 2015 in Cambridge, Jamie Savan gave a strikingly impressive presentation arguing that original cornetti differ in important respects from their modern reproductions, the design of the latter now beginning to reveal shortcomings as a result of an improved understanding of the mechanical structure, optimal fingering systems and blowing regime for the originals.
Here are two fairly old instruments:
The first is a French 19th century chanter by Jean Sautivet, measuring 19.5 pouces, 540mm, so approximately in D (all fingerholes but lowest closed); boxwood. (Ref. 2)
The second is an original renaissance tenor recorder, speaking length about 556mm; boxwood. (Ref. 3).
Note in both instruments the relatively consistent sizes and regular spacing of the fingerholes.
It hardly needs saying that we know from originals and modern reproductions that these instruments are capable of playing well tuned scales, including major and minor thirds, as of course were the whole range of early woodwinds. For this reason I think it would be unwise to assume the use of a neutral third without being able to undertake a thorough assessment of the performance of an instrument, using not only the correct fingering, but also an optimum reed and set-up if appropriate.
On the origins of the cabrette, Michel Esbelin says: “………… one cannot give credit for the invention of the cabrette to any particular pipe-maker. All we know is that it was born and then developed in Paris [at the end of the 19th century].” This work was carried out by immigrants from the Auvergne who brought the ancestors of the cabrette with them from their region, instruments no doubt related to the musettes or cornemuse du Centre. He suggests that the design of the cabrette may have been drawn from features both of the latter and (in particular as regards the stock system) of the musette de cour. (The translation somewhat whimsically to our ears refers to the stock system of the musette de cour as a “box with balls”………).
Bearing this in mind, and the fact of the three-finger tonic, there does not either seem to be much ground for arguing that the tuning of the cabrette could have been influenced by Arabic scales. In its heyday, the cabrette was played solo, without drone. The repertoire was dance-music, much of it in a rapid tempo. It was not required to be in tune with anything, and the fact that the interval from the sub-tonic to the tonic was wide was exploited and used to create a personal style.
Ray also refers to the use of microtones in early music, and cites Guillaume Costeley’s “Chromatic Chanson” Seigneur Dieu ta pitié of 1558. At the website reference given by Ray, the explanatory text states that Costeley became interested in an Archicembalo constructed by the Italian musician and theorist Nicolo Vicentino which possessed 19 notes per octave. Now a 19 tone equal temperament can be constructed from a cycle of 19 fifths in order to allow closer approximations to consonance than a 12 tone cycle, and this is in fact what Costeley specified. What he was interested in was not microtonal intervals as we might hear them for example in Arabic music, but in order to give him a great choice of consonant intervals as the context of the music demanded. If he had had a viol consort to hand, he could have heard the same piece played perfectly in tune, and microtones would not have come into it. So I don’t think that this use of microtonal intervals can give us any help in finding an origin for unusual scales.
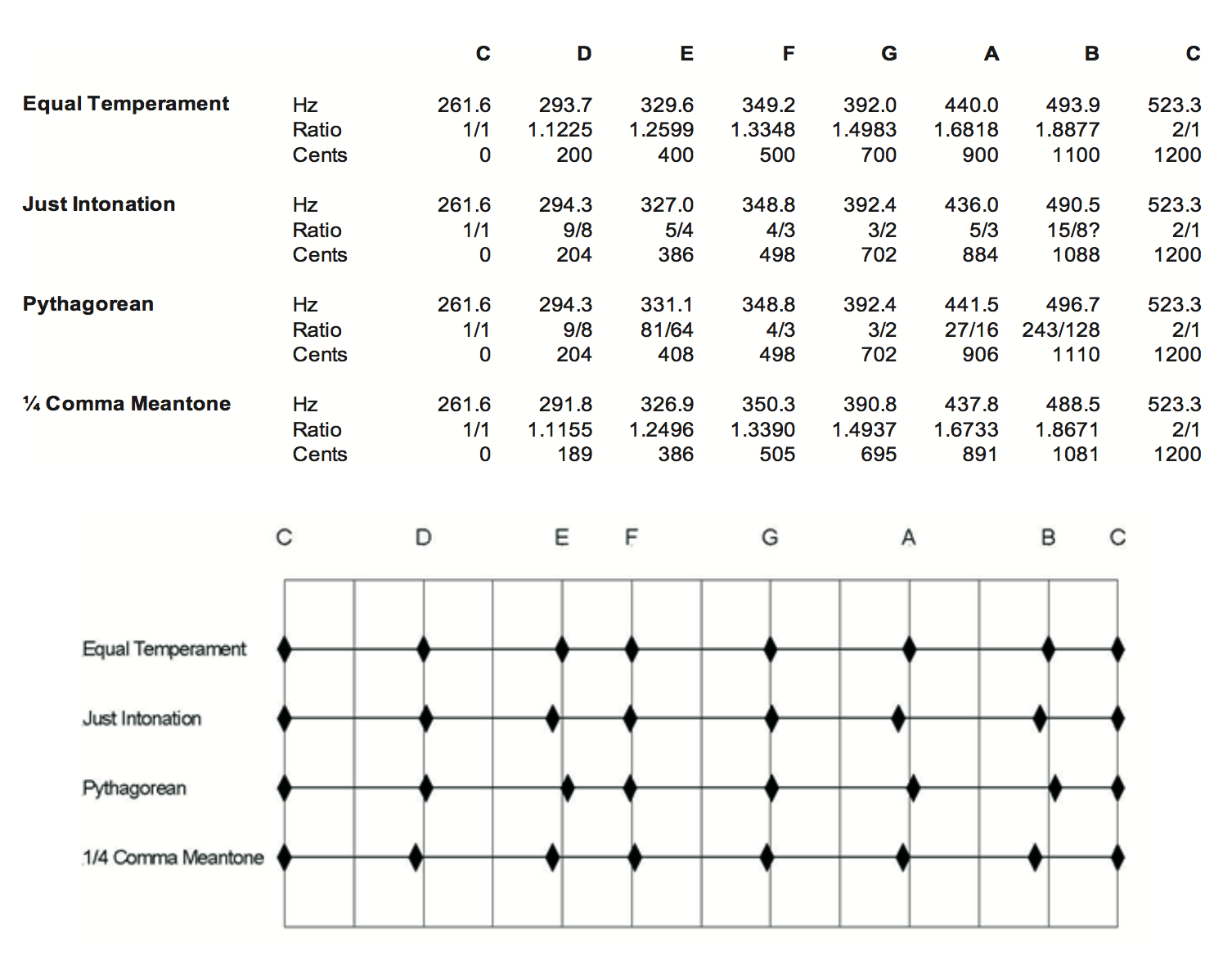
Turning to the question of bagpipe scales in general, in his fourth paragraph, Ray says: “Just Intonation is an overall term for tuning systems such as Pythagorean, meantone etc . . . . . .”
This is not correct. A just scale, a Pythagorean scale and a meantone scale are all different. I have written previously in Chanter or the Newsletter about the modern pipe scale and how it is derived in my incarnation as Uncle Octavius. See Pipersʹ Problem Page, Newsletter, 14th January 1989. John Tose also talks about it in Chanter Spring 2007.
Just Intonation produces a scale in which each note is derived from a small whole-number ratio with the tonic; so: Tonic 1/1, major second 9/8, major third 5/4, perfect fourth 4/3, perfect fifth 3/2, major sixth 5/3, major seventh 15/8 (?), Octave 2/1. This is the system which I suggest modern makers use for tuning pipes of what have been referred to as the ‘Europipe’ variety, but also for Northumbrian Smallpipes, for example . It means that each note will have maximum consonance (beat free relationship) with the tonic (drone). (I have put a query against the seventh because where you can play both a major and minor seventh, the latter being cross-fingered, there is usually a compromise tuning in order to allow the tuning of both to be acceptable). Since the frequency of harmonics are whole-number multiples of the fundamental (first harmonic), there is a sense in which this chanter scale is contained within the drones. When we tune our drones, we are listening for maximum consonance and minimum beating between one or more harmonics of the drone(s) and the chanter note.
The Pythagorean scale is derived by stacking perfect fifths upon each other, dividing by two if necessary to bring the note within the octave. See the diagrams below. Note that while the fourth and fifth are true, the third and sixth are sharp, even more so than with Equal Temperament.
Meantone Temperament: there are loads of them and there’s no room to go into that here. Prior to the introduction of Equal Temperament, they were devised as systems for tuning keyboards in order to be able to play acceptably in tune within a rather narrow range of keys. A temperament called 1⁄4 Comma Meantone was popular in the 16th and 17th centuries, and according to Lloyd and Boyle (Ref. 4) (my bible on such matters) remained in use in this country for tuning organs well into the 19th century. This was chosen because it gives well- tuned thirds and sixths. Simplifying more than somewhat, this was achieved as follows: taking four perfect fifths above the tonic (eg C-G-D-A-E) brings you to a third which is sharp of a just third by a small interval which was called a comma and equal to about 21 cents. (100 cents to the equally tempered semitone). The four fifths were each tuned smaller than perfect by one quarter of the comma, bringing the third into tune. Read more about it in Lloyd and Boyle or Wikipaedia, though the former is easier to understand and less theoretical. The drawback of the system is that it cannot be made to work in all keys so modulation into all keys is not possible. As Lloyd and Boyle say: “……. we have no Db, D#, Gb, A, or A#. If we try to use C#, Eb, F#, G# or Bb instead, we shall produce what our great grandfathers called a ‘wolf’ because of its howling.”
Hence the subsequent development of equal temperament, with its less well- tuned thirds and sixths, but complete freedom of modulation.
The tables below show a diatonic major scale of C, that is to say, the white notes on a keyboard. This is key is chosen for simplicity and for ease of visualisation, even though many if not most of our pipes will be in a key other than C. However they are pitched, many if not most of our pipes will be able to play the same major scale with the same qualification regarding the seventh referred to above. There is no particular reason for choosing a major rather than a minor seventh.
The tables show the information both numerically and graphically. The grid is laid out to suit equal temperament. That is to say that there are twelve intervals equally spaced, but as stated above only the seven notes (eight including the octave) of the diatonic major scale are shown.
The first two scales are the ones of most interest to us, corresponding in the case of the Equal Temperament scale to the modern keyboard scale, and in the case of the Just scale to a chanter scale. Note in particular how these two scales differ in the tuning of the third degree of the scale (E), 14 cents, and of the sixth (A), 16 cents.
The idea that modern scales developed from the harmonic series as revealed by the wooden folk trumpet (tulnic) is an interesting one, but does not account for the fact that the voice must have predated all other instruments by a long way . The intervals of the octave, fourth, fifth, major third, minor third and major second are all contained in the lower reaches of the harmonic series, but as far as I know no one actually sings using the sequence above, say, the tenth harmonic. Arthur Benade (Ref. 5) has shown that we are physiologically wired to recognise consonance. The explanation of Just Intonation above shows how a justly tuned diatonic scale on a bagpipe chanter is derived from the sound of the drone(s). So when Ray says: “It would not be unreasonable to suggest that chanter tuning would be done to harmonise the drone harmonics and so would include intervals outside our currently accepted scales”, I could not agree more, except to say that those intervals are far from being outside our currently accepted scales. Not only do they form a just scale, but the intervals are used all the time when musicians sing or play in tune with each other, unless they are striving to sing or play in tune with a fixed pitch multiphonic instrument such as a keyboard or accordion tuned (as the vast majority are) to Equal Temperament.
The findings of Alexander Ellis regarding the MacDonald chanter (early 1800s) in which the third (C) is low contrast with those of Barnaby Brown in his investigation (with Julian Goodacre) of the Ian Dall chanter (Ref. 6) where he says: “Crucial to the question of intonation is fingering, which has an effect that varies from reed to reed………..Although the ‘closed’ fingering for C [x xxx xoo x] fell out of general use in the 19th century, David Glen wrote in 1881 that, ‘when fingered in this way the C is sharpened and rendered more perfect’.” He quotes the treatise of Joseph MacDonald (1739-63) who “certainly perceived C as a major third, and wrote ‘There is no natural C or F in the Bagpipe Scale…..The Key for Laments excludes C altogether because it is sharp.’”
I can’t leave Alexander Ellis without quoting a footnote in Lloyd and Boyle (my impression is that they disapproved of Ellis as a ’theorist’ who neglected musical considerations, and I like to detect a feeling of relish in this quotation) “A footnote by Hipkin’s daughter to the article on Ellis in Grove [Dictionary of Music] III & IV reads as follows:- ‘Ellis’s exhaustive experiments were made entirely by calculation, as he was tone-deaf and unable to distinguish one tone or tune from another. Hipkins tested each experiment by ear.’” However, what follows the above in Barnaby Brown’s examination of the Ian Dall chanter, is a fascinating discussion of bagpipe and related scales and the merits or otherwise of tunings which depart from consonance with the drones. The Ian Dall chanter was found to have a scale broadly corresponding with just intonation, including a so-called harmonic seventh, but with a fourth sharp by about 20 cents. Barnaby characterised this type of fourth as ‘colourful’, and perhaps it’s an example of the ‘wildness’ the loss of which was regretted by Andy Letcher. The sharp fourth was apparently characteristic of highland chanters until comparatively recently; in recent years the chanter scale has been converging on consonance, but there are some signs that this may be changing again in subtle ways.
To sum up, I am aware that Ian’s original question: “Cabrette Tuning, What’s it all about?” or why has the cabrette retained a tuning different from modern cornemuses du Centre, has not really been answered. Barnaby Brown puts it well when he says: “The interaction of cultural and physical factors giving rise to the intonation ideals of an individual or tradition is a complex and capricious subject.” Ian was attracted to the cabrette for its unique voice, a component of which is the tuning of its scale. Part of the answer is that the ‘offending’ note, the low sub-tonic, is not part of any harmonic scheme with which it might seek to become in tune. The instrument was played solo without drone; there is no collateral motive or constraint to push the tuning otherwise. Indeed the musicians who created the early tradition seem to have capitalised on this feature of the tuning as part of developing a personal style. In trying to reach an answer, I have tried to clarify the way in which it seems to me that the cabrette functions musically, and to respond to some questions posed by Ray’s article particularly with regard to the scales and harmonic structures within which pipes and pipers work.
References:
- The Cabrette d’Auvergne. A town or country musette? Michel Esbelin. Proceedings of the International Bagpipe Symposium. 17th September 1888, The Hague, Netherlands.
- Les Cornemuses de George Sand. Museum Catalogue. Musées de Montlucon 1996. Plate No 37. Chanter of a set of engraved horn-mounted bagpipes by Jean Sautivet, 19th century. B Blanc collection. Boxwood, lead and two coloured horn.
- Die Renaissanceblockflöten der Sammlung alter Musikinstrumente des Kunsthistorischen Museums, Vienna. Beatrix Darmstädter and Adrian Brown. Plate labelled SAM 151. Instrument came to the collection from Catajo Castle near Padua, built in 1573.
- Intervals Scales and Temperaments. Llewellyn S. Lloyd and Hugh Boyle. An introduction to the study of musical intonation. MacDonald and Jane’s. 1963.
- Fundamentals of Musical Acoustics. Arthur H. Benade. OUP. 1976.
- The Ian Dall Chanter: Material Evidence for Intonation and Pitch in Gaelic Scotland 1650-1800. Barnaby Brown. Published in The Highland Bagpipe, Music History Tradition. Edited by Joshua Dixon. Ashgate. 2009.
- Data Processing Notice (GDPR)
@BagpipeSociety on X (formally known as Twitter)
TheBagpipeSociety on Instagram
 BagpipeSociety on Facebook
BagpipeSociety on Facebook
Something wrong or missing from this page? Let us know!
